Semiregulaarinen monitahokas

Semiregulaariset monitahokkaat::
Arkhimedeen kappaleet sekä joukko särmiöitä ja antiprismoja

Semiregulaarinen monitahokas on avaruusgeometrinen termi, jota eri kirjoittajat ovat käyttäneet hieman eri merkityksissä.

Alkuperäisen määritelmän mukaan semiregulaarinen on monitahokas, jonka tahkot ovat säännöllisiä monikulmioita ja jonka symmetriaryhmä on transitiivinen kärkien suhteen, toisin sanoen se voidaan aina kuvata yhtenevyyskuvauksella itselleen niin, että mikä tahansa sen kärjistä voi kuvautua mihkä tahansa toisen kärjen kohdalle. Tässä merkityksessä nimitys perustuu Thorold Gosset'n vuonna 1900 esittämään yleisempään semiregulaarisen polytoopin määritelmään.^[1][2] Nykyisin tällaisista käytetään kuitenkin yleisemmin nimitystä uniforminen monitahokas. Uniformisia eli tässä merkityksessä semiregulaarisia ovat:^[3][4]

• kaikki 13 Arkhimedeen kappaletta
• ääretön sarja kuperia särmiöitä
• ääretön sarja kuperia antiprismoja, joiden semiregulaarisen luonteen pani ensimmäisenä merkille Kepler.

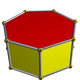
Nämä semiregulaariset kappaleet voidaan täysin määrittää kärkikuviolla eli luettelemalla sivujensa lukumäärän mukaan ja sijaintiensa mukaisessa järjestyksessä ne tahkot, jotka kärjessä kohtaavat. Esimerkiksi 3.5.3.5 esittää ikosidodekaedria, jossa jokaisen kärjen ympärillä on vuorotellen kaksi kolmiota ja kaksi viisikulmiota. Sen sijaan 3.3.3.5 tarkoittaa pentagonaalista antiprismaa. Näitä monitahokkaita sanotaan joskus kärkitransitiivisiksi.

Gosset'n jälkeen muut kirjoittajat ovat käyttäneet termiä semiregulaarinen varsinkin korkeampiulotteisten polytooppien yhteydessä eri merkityksissä. E. L. Elte ^[5] esitti määritelmän, jota Coxeter piti liian keinotekoisena. Coxeter itse nimitti Gosset'n semiregulaariksiksi nimittämiä kappaleita uniformisiksi kappaleiksi, joista hän nimitti semiregulaariksi vain hyvin rajoitettua osajoukkoa.^[6]

Toiset sen sijaan ovat päin vastoin laajentaneet semiregulaarisen monitahokkaan käsitettä luokittelemalla sellaisiksi eräitä muitakin kuin edellä mainitut. Sellaisia ovat:

• Kolme joukkoa tähtimonitahokkaita, jotka toteuttavatkin Gosset'n määritelmän ehdot ja ovat analogisia edellä luetelluille kuperien monitahokkaiden joukoille.
• Edellä mainittujen semiregulaaristen monikulmioiden duaalikappaleet sillä perusteella, että niillä on samat symmetriat kuin edellisillä. Näihin duaalikappaleisiin kuuluvat Catalanin kappaleet, kuperat dipyramidit ja antidipyramidit eli trapetsoedrit sekä niiden ei-kuperat vastineet.

Lisää sekaannusta aiheutuu siitäkin, millä tavoin Arkhimedeen kappaleet on määritelty, sillä niistäkin on erilaisia tulkintoja.

Gosset'n määritelmän mukaan semiregulaarisiksi katsotaan nekin kappaleet, joilla on vielä suurempi symmetria, kuten säännölliset monitahokkaat eli Platonin kappaleet sekä kvasisäännölliset monitahokkaat. Joidenkuiden myöhempien kirjoittajien mukaan näitä ei pitäisi sanoa semiregulaariksi eli "puoliksi säännöllisiksi", koska ne ovat vielä säännöllisempiä: termiä uniforminen monitahokas käytetään tällöin kattokäsitteenä, joka jakautuu kolmeen ryhmään: säännölliset, kvasisäännölliset ja semiregulaariset monitahokkaat. Tätä nimeämisjärjestelmää käyttämällä vältytään monilta, joskaan ei kaikilta sekaannuksilta.

Käytännössä sekaannusta esiintyy pätevimmilläkin kirjoittajilla, jotka määrittelevät jonkin monitahokkaiden joukon semiregulaariseksi tai Arkhimedeen monitahokkaisiksi, mutta käyttävätkin näitä termejä myöhemmin laajemmasta tai suppeammasta monitahokkaiden joukosta, kuin alun perin määrittelivät niiden tarkoittavan. Esimerkiksi joukkoon luetaan myöhemmin vain kuperat monitahokkaat, vaikka niin ei määritelmässä sanottukaan. Tämän virheen ovat tehneet muun muassa Coxeter ja Cromwell^[7] sekä Cundy ja Rollett.^[8]

1. ↑ Thorold Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions. Messenger of Mathematics, 1900. Macmillan.
2. ↑ H. S. M. Coxeter: Regular polytopes (3rd ed.). Dover, 1973.
3. ↑ Semiregular Polyhedron Wolfram MathWorld. Eric W. Weisstein. Viitattu 9.11.2018.
4. ↑ Semi-Regular Polyhedron Mathmos.net. Viitattu 9.11.2018.
5. ↑ E. L. Elte: The Semiregular Polytopes of the Hyperspaces. Groningen: University of Groningen, 1912.
6. ↑ Uniform Polyhedra. Philosophical Transactions of the Royal Society of London, 1954, nro 246 A, s. 401–450. Artikkelin verkkoversio.
7. ↑ P. Cromwell: Polyhedra. Cambridge University Press, 1997.
8. ↑ H. M. Cundy, A. P. Rollett: Mathematical models, 2nd ed. Oxford University Press, 1961.